Cách check mã vạch để xem độ chính xác (P2)
- Jul 5, 2019
- 7 min read
Updated: Aug 1, 2019
Ở phần một trước đó mình đã nói về cách check mã vạch cho các loại mã 1D rồi. Nên lần này mình sẽ cố gắng đi vào các loại mã vạch 2D cho bạn luôn. Căn bản là các loại mã vạch này khó hiểu hơn nhiều so với mã 1D. Nên việc giải thích hết một lượt bên đó có thể sẽ làm bạn rối. Nếu bạn tình cờ không có những công cụ giúp check mã vạch ở đó thì cách này có thể giúp bạn. Cùng đi vào cách tính mã vạch 2D để kiểm tra độ chính xác.

Chi tiết về cách check mã vạch 2D
Trước khi vào cách tính mã vạch 2D, bạn cần ghi nhớ một điều. Đó là bạn sẽ phải giải mã các mã 2D này. Bạn sẽ không thể nào tính được số check lỗi nào của các mã 2D đâu. Lý do là vì chúng đi theo một công thức toán học vô cùng phức tạp có tên gọi dưới đây.
1. Reed-Solomon-Error correction
Đây là một loại tính số check lỗi và sửa lỗi vô cùng công phu được phát hiện năm 1960. Nó được áp dụng cho mã QR code nhằm khắc phục một số trường hợp mã bị mất 1 phần hoặc che. Nếu có trường hợp này xảy ra thì các phần Error Correction (EC) sẽ hỗ trợ máy quét mã vạch 2D đọc được các mã.

Nếu bạn nhìn công thức của Solomon EC này trên Wiki thì nó quá phức tạp. Nên trừ khi bạn là người giỏi toán vô cùng thì không nên thực hiện cách check mã vạch này. Các mã 2D từ PDF417 đến Data Matrix và Aztec Code đều đi theo đúng phương pháp kiểm tra lỗi này.
2. Cách check mã vạch QR Code
2.1. Xác định mask pattern và đảo mã
Để đi vào một mã vạch QR và check độ chính xác của nó, bạn cần không ít thời gian đâu. Bạn đầu tiên cần phân biệt vùng mã sử dụng để giải mã. Sử dụng thử đoạn mã Robomatics này để làm xem sao nhé. Bạn cần excel để có thể làm việc này một cách tự nhiên và dễ hơn. Qua trình mất thời gian là chuyển mã này lên các ô excel để thao tác. Như bạn thấy trong hình số 1 mình chuyển lên bên dưới.

Sau khi chuyển xong thì mình xác định mask pattern của mã. Mask pattern là một dãy cấu tạo được tạo ra và chèn và mã. Giúp tránh cho một đoạn mã hình thành bị giống Finding Pattern hoặc các phần cố định khác. Ở đây phần mã xác định mask pattern là như hình số 2. Ở đây là đen, trắng, trắng hay là (1,0,0). Nên dựa theo mask pattern bạn so sánh trong LINK thì phát hiện ra là j % 3 = 0. Tiếp đó bạn đánh dấu những đoạn mask xám từ dưới lên như hình 3. Nếu gặp timing pattern và các phần cố định được đánh màu thì bỏ qua và tiếp tục sử dụng mask pattern lên các dòng còn lại.

Sau khi xong bạn lồng đoạn mask xám vào code ban đầu ở excel.
2.2. Cách check mã vạch QR Code – Giải mã
Sau khi lồng code vào, bạn xem những nơi có pattern xám bạn vẽ chạy qua. Ô nào có màu đen thì đảo thành trắng, và ngược lại. Sau khi làm xong rồi bạn sẽ có được như hình dưới.

Nhìn vào góc phải bên dưới của code đã đảo mã, lấy 4 ô đầu tiên. 4 ô này để xác định dạng mã hóa có trong mã QR này là gì (byte, alphanumeric, vv..). Bạn có thể xem bảng sau để xác định chúng.
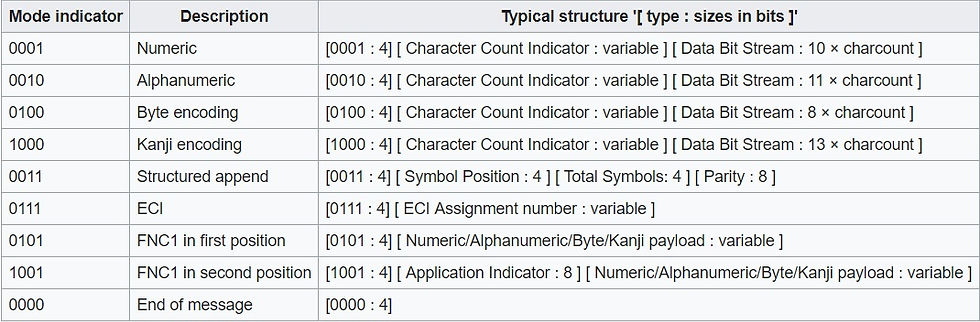
Dựa vào trường hợp đoạn mã này thì là 0100 là byte. Tùy theo loại dạng mã hóa mà bạn sẽ đối chiếu các cột khác nhau trong bảng kí tự ASCII sau này.
Sau khi xác định xong kiểu mã hóa, thì dựa theo kiểu mã hóa này, thì bạn có sơ đồ như sau (nguồn wikipedia).

Theo hình thì kí tự đầu tiên của bạn sẽ bắt đầu bằng chuỗi kí tự thứ 2 sau Len. Len là độ dài của bit có trong mỗi chuỗi. Bạn nhìn vào bit order, số 1 là số quan trọng nên để bit có giá trị lớn nhất là 128. Sau đó đi dần từ 2 đến 8 lần lượt là 64, 32, 16, 8, 4, 2, 1. Xoay ngang và dọc theo chiều mũi tên như sơ đồ sẽ có cách sắp xếp khác. Bạn đọc mã luôn đi theo đường zig zag như hình.

2.3. Tính và quay đổi mã số ra chữ cái
Nhìn vào ô sau len. Bạn thấy và đối chiếu với cách sắp xếp giá trị bit. Bạn xem những ô nào là đen thì cộng giá trị bit ở ô đó vào. Sau khi cộng ra kết quả rồi thì đối chiếu nó với bảng giá trị ASCII. Đang là Bite nên bạn nhìn vào cột Decimal và đối chiếu sang kí tự. Ở đây là 64 + 16 + 2 = 82. Đối chiếu là kí tự R (viết hoa). ASCII có phân biệt chữ hoa chữ thường.

Làm dần đến khi bạn đến đoạn bit tương đương với chữ s thường. Bạn nhìn sau nó là 4 ô trắng, biểu thị 0000 đó là mã kết thúc của đoạn kí tự được mã hóa. Phần đằng sau chính là các số Error Correction tính theo thuật toán Solomon mình nói ở trên. Khi xong bạn có thể check kết quả khi có cơ hội gặp được máy đọc mã để kiểm tra.

Cách làm này áp dụng tương tự cho những Mask Pattern còn lại. Chú ý khi bạn gặp đoạn mã có Align Pattern (ô vuông nhỏ hơn finding pattern nằm ở góc phải bên dưới), thì mã sẽ có kết cấu interleaved như hình sơ đồ.

3. Cách check mã vạch Data Matrix
Ngoài mã QR, thì Data Matrix cũng được sử dụng rất nhiều trong các ngành công nghiệp. Nên mình cũng cố gắng đề cập đến nó trong bài này. Những mã khác như Aztec hay PDF417 cũng không phải dễ dàng. Nên chắc là 2 mã này cũng đủ làm cho bạn rối rồi. MÌnh thử dùng mã ABCabc123 và mã hóa nó thành Data Matrix. Và nó có hình dáng như sau.

Nếu bạn đọc về cấu tạo mã 2D hoạt động thì bạn sẽ thấy nó phân thành các square (hoặc chunk tùy người gọi) hình chữ L và có cấu tạo chi tiết như hình phía dưới. Nào, để ý là có những phẩn không theo chữ L 8 ô chuẩn mà nó sẽ bao quanh những phẩn thừa còn lại. Và cấu tạo thứ tự từ 1 cho đến 18. Số lượng thay đổi tùy theo độ lớn của mã. Mã mình đang dùng là 14 x 14 pixel.

Trước mắt khi bạn nhìn vào 1 mã thì bạn nên cố gắng tìm những chữ L hoàn chỉnh trước. Để ý là theo sơ đồ thì số 2 luôn L chữ L hoàn chỉnh đầu tiên và số 1 không hoàn chỉnh nằm ngay phía dưới. Bạn cũng nên để ý số 8 nằm ở góc phải phía trên. Góc này sẽ thay đổi tùy theo độ lớn, nên bạn đừng nao núng khi gặp mã khác mà không có hình dáng tương tự. Bạn có thể tham khảo các trường hợp này ở Wikipedia.
3.1. Đi vào cách check mã vạch Datamatrix
18 khung này chỉ có 8 ô là chứa các kí tự được mã hóa. 10 ô còn lại là Error Correction tuân theo mã Reed- Solomon. Khung mã được cấu tạo theo các số 128 – 1. Và nó đi dần theo cấu tạo như hình dưới. Từ trường hợp số ở góc phải trên (trường hợp này là 8) thì bạn phải lấy cách sắp xếp số từ 1 đến 8. Data Matrix ngược với QR ở chỗ số lớn nhất là số quan trọng nhất. Nên 8 sẽ là 128, và 1 sẽ là 1.

Các mã Data Matrix có những số bit đại diện cho nhiều loại kí tự khác nhau. Nhưng đa số sẽ dùng ASCII cho bit 8. Nên mã này mình dùng đến ASCII 127 (0 – 127). ASCII mã hóa theo loại nào mình sẽ nói chi tiết sau.
Sau khi phân thành các square và đánh số bit như hình trên xong. Bạn bắt đầu tính để giải mã. Nhìn vào chunk thứ 1. Các ô đen nằm ở các số 64 và 2. Nên là 64 + 2 = 66. Lấy số này trừ đi 1 (do đang tính ở ASCII 0 – 127, nếu từ 1 – 128 thì bạn không cần trừ 1). Kết quả là 65. Đối chiếu với bảng ASCII 127 thì là kí tự A viết hoa. Bạn đi đến hết chữ c thường.
3.1.1. Trường hợp đặc biệt
Đến ô số 7 này kết quả cộng quá 128 (hay quá 130). Thi trường hợp này bạn lấy kết quả 142 – 130 = 12. Thì 12 ở đây là 1 và 2. Người thiết kế ra mã này đã thiết kế như vậy. Bạn không cần đối chiếu bảng. Khi gặp 2 số (chỉ số thôi) là 2 số liên nhau, thì kết quả cộng luôn lớn hơn 130. Để bạn trừ đi và ra kết quả là 2 số kế nhau ghép lại.

Đến kí tự cuối là 3, thì là kí tự bạn so sánh với bảng là 51 chính là số 3. Và cuối cùng là bạn có mã của mình. Các chunk sau đó bạn cũng không cần quan tâm đến nữa.

Vậy nếu sau có kết quả là 129? Nếu bạn gặp số này có nghĩa là bạn không cần quan tâm đến các chunk sau luôn. GS1 có bảng chi tiết về Data Matrix này. Độ lớn của mã sẽ có bao nhiêu Chunk là EC hoặc dữ liệu mã hóa. Đó là cách thông thường để bạn check mã vạch Data Matrix.
Xong bài về cách check mã vạch này bạn có thấy rối chưa? Đó là 2 mã căn bản thông dụng của mã 2D đấy. Aztec và PDF417 là vô cùng phức tạp. Và mình sẽ không cố gắng đi vào nó đâu. Vì thật sự ra nó cũng như mình cố chỉ bạn về Reed-Solomon vậy. Mong rằng bài này sẽ cho bạn bức tranh về mã 2D này, và lý do tại sao nó phức tạp và bảo mật như vậy.








































Comments